iPhone 一直都是关于屏幕，Steve Jobs 在 2007 年发布会上就将第一代 iPhone 的 3.5 吋显示屏称为“巨大的屏幕”，而在 iPhone 设计最初阶段也同“无边泳池”这个意象相关联，所有的设计元素遵从于屏幕而不能让用户分心，全屏幕设计的 iPhone X 将对这一理念的执行提到具有划时代意义的高度之上，由 iPhone X 划分前后两个时代。

但是仅一块大屏幕无法开启未来，屏占比和边框宽度之类的参数指标无法用来作为时代划分的依据，用户的认知并非受控于一些参数条，从 89% 增大到 90% 对用户来说并没有质的改变。质的改变必须作用于用户的认知，不是用语言上的假象或者宣传手段来说服，而是用真象和产品，递出一把钥匙，也就是设计。

一个革命性的产品背后有大量的技术的支撑，每一处创新的实现背后又有大量的繁杂的具体工作，但是用户认识到的却是产品的“外在形象”，这个外在形象具有自明性，并非技术使然，用户认识到的产品的外在形象与技术无任何关系，比如用户认识到的手机就是它的外在形象，手机里面的 CPU 或者制作这款手机的工艺等对用户来说没有意义，因此，设计师工作的两面性在于，台前，需要将外在形象与背后的技术相隔离开，幕后，则需要为实现这个外在形象去与背后的技术形成关联。我们看到的那些炫技的设计，就是设计师期望外在形象与背后技术形成关联，以及我们经常能见到的那些以参数为目标的设计，也是如此。

产品的外在形象越简洁越易识别，越脱离技术关联就越有说服力。

很多手机厂商在宣传自己的大屏幕手机时，总会使用到一个手段，比如是平面广告还是视频上，那就是让手机屏幕内的内容与所处的背景融合在一起，让人感觉手机消失了，或者说边框消失了，这种宣传手段在强调的恰恰是手机的技术参数一面，而与“外在形象”没有太大关联。

iPhone X 上脱离了技术关联的就是全屏幕，而塑造 iPhone X 的全屏幕外在形象最重要的设计特征就是四个圆角。柔性 OLED 屏幕的切割和折叠，相应的电路堆叠技术，或者是圆角处的次像素反走样渲染等等技术内容，对厂家来说，可以用此辅助来向用户说明自己创新的独特之处，但对于用户来说，真正关心的只有外在形象，也就是这块独特的圆角全面屏。通常来说，如此大的圆角的屏幕是反技术的，不符合技术的理性导向，也就是为什么它需要更多额外技术支撑的原因，但在产品之上，在用户关心的外在形象之上，这个圆角屏幕却是非常自然的结果，依照手机的形态形成的均一的屏幕外轮廓符合全面屏的概念；而另外一面，突破常规的形象（屏幕总是四四方方的）则又能表现出它的革命性。

Apple 标志性的圆角曲线在 iPhone X 的应用，将其划时代的意义通过外在形象向前推了一大步，并与其他厂家的类似产品形成差距，人们将进一步认为 iPhone X 才是真正的全面屏，而其他的设计，如屏幕的外轮廓没有追随机身形态，都会被认为不够彻底的。与此同时，如果屏幕的圆角很小，它就更像一个技术革新产品，无法脱离技术关联感，也就是无法为用户的认知带来革新。在 iPhone X 上，屏幕的圆角，以及因这个圆角形成的整体形象的重要性，从 Apple 对屏幕上端的缺口处理就可以得到验证。从 Apple 的产品图和宣传资料上看，对屏幕的缺口（Notch）不仅毫无掩饰，而且还加以强调和渲染，为突出 Face ID，为形成一个标志性的视觉元素，也是以不避讳的方式在强调全屏幕形象。我们甚至可以确定，iPhone X 上端屏幕缺口两侧的圆角区域，就是为了营造“外在形象”，从功能、技术和理性层面来说，更倾向于将屏幕上端做齐平而无缺口，这个外在形象是如此重要，Apple 甚至在软件界面上也不去对这个缺口作过多的掩饰。

如我们所知，从 iOS 开始，Apple 将产品上的圆角曲线应用到界面之上，主要是围绕着圆角四边形的图标上，而从 iPhone X 上的 iOS 11 上可以看到，在界面上加入了更多圆角曲线的元素，就像上图所示的一角所展示，从外到内，形成了一层层更加连续的多度，从最外侧的圆角开始一直等距递进到电话图标，如果去仔细核算，这个角落可以数出至少 7 条等距圆角曲线。

到处都是圆角。

早期的计算机采用的是 CRT 显示器，而 CRT 显示器是用真空玻璃管做成的，要保证它的安全和密闭性，以及可制造性，CRT 显示器玻璃要做成凸面的，而且四周的外轮廓并非四四方方，而是向外凸的弧线形成的四边形，四个角当然就为圆角，所以，早期的 CRT 显示器基本都是外凸并且四角都有大圆角。

上图分别是 1981 年的 Xerox Star 8010 和 1984 年的 Macintosh 电脑，可以看出当时围绕着屏幕的设计是如何抵消弧面屏幕的反直觉性，通常的方式就是用罩壳圈出一个相对四方的显示区域，比如 Xerox Alto 那样，而四角的圆角处理可以让显示区域显得更平（因为四角形态收缩更厉害）。Xerox Star 8010 在罩壳下都为内容显示区，而 Macintosh 则有大的黑边，内容显示区域面积更小也更为平坦，Macintosh 上的这个黑边为界面显示黑色，并非显像管上的非显示区，与“用黑色来掩盖 iPhone X 上的屏幕缺口”同理。

Macintosh 界面四周有小小的圆角，可以看出是经过设计的圆角。

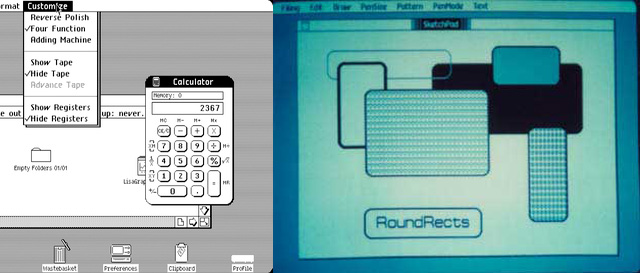
左图为 1983 年发行的 Lisa Office System 3.1（图片来自 Wikipedia），可以看到界面的四角，以及计算器的界面轮廓都出现了圆角四边形。

按 Andy Hertzfeld 在 The Original Macintosh 中所写，Apple 在软件界面上出现圆角四边形可以追溯到 1981 年，Andy Hertzfeld 在 Round Rects Are Everywhere! 这一节中说到了圆角四边形诞生时的故事。当时 Apple 的天才程序员 Bill Atkinson 正向团队展示他是如何用一种聪明的方法可以在仅有 68000 处理器的 Lisa 和 Macintosh 机器上快速画出圆和椭圆，Steve Jobs 看了之后有另外的想法，他说：“圆和椭圆都不错，但是能画出带圆角的四边形吗？我们现在也能画出吗？” Bill Atkinson 回答说很难做到，而且他认为并不真需要圆角四边形，Steve Jobs 就立刻强烈回应了：“到处都是圆角四边形！看看这个房间周围就知道了！”并且还带着 Bill Atkinson 出去转看可以碰到多少圆角四边形，最后 Bill Atkinson 被说服，第二天下午就拿出了满意的结果。

接着，圆角四边形在 Apple 的软件界面上到处都是了。

iOS 的圆角图标

2013 年随着 iOS 7 的发布，Apple 将 iOS 上的标志性的圆角图标轮廓作了更新，将工业设计中的曲线连续概念应用到了视觉设计之上，iOS 7 之前的圆角图标，也包括通常的平面设计软件中绘制的圆角四边形，圆角部分为一段圆弧，那么在直线和曲线的连接点处曲率从 0 立刻过渡到一个恒定的数值，带来的视觉感觉就是过渡不顺畅，保证顺畅就需要让直线到曲线过渡中形成一个连续的变化，从 0 逐渐地过渡到某个数值，而不是从 0 跳动到某个数值。在实际操作中，并非一件简单的事，曲线的过渡也是一件讲究技艺的事，也要求一定的数学意识。

iOS 7 在介绍新的圆角图标轮廓时，给出了上图右的一张线框示意图，图中在圆角处密密麻麻的点让人感到困惑，并非难以逆向破解，由于最近 Apple 在 UI Design Resources 上给出了 iOS UI 素材的下载，里面包含了这个圆角图标轮廓的矢量图，我们可以通过这个矢量图可以挖掘到一些信息。

简单的概念

在前文《J 的艺术，R 的艺术》已经对曲率连续一些基本概念作过介绍，在此稍作重复一下。

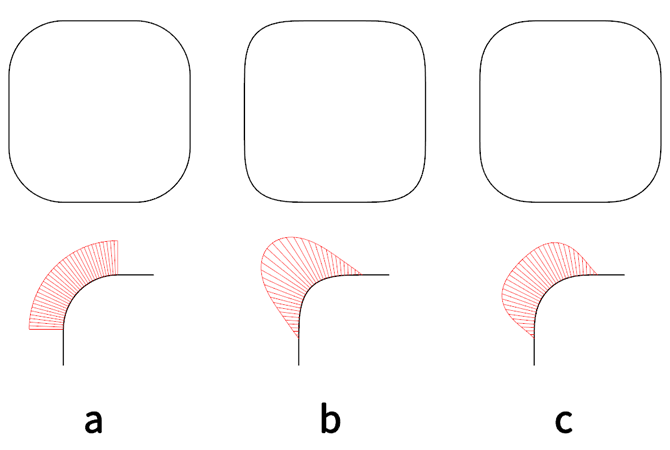
上图 a 为 1/4 圆弧过渡的圆角，iOS 7 之前的圆角图标，通常平面软件绘制的圆角四边形，以及通常我们称作“导圆角”，都为上图 a 所示的方式。因为直线的曲率为 0，而圆弧的曲率为一固定值，所以从直线到圆弧有曲率的突变，虽然是切线连续（G1 连续），但是无法达到曲率连续（G2 连续），这种过渡的不顺畅我们可以通过视觉很明显地感觉到。

上图 b 为用一段曲线替代了 1/4 圆弧作过渡，绘制时要求连接直线的两端达到曲率连续，即这段曲线的曲率是从两端的 0 逐渐连续的增大的，我们能够从图形的四个角上看到过渡顺畅，但是，存在一个问题就是，看上去四个角不够圆了。虽然光滑但不够圆，我们也可以从曲率的示意图中观察到，这条曲线曲率的变化不具备圆的特征，因为圆的曲率处处相等，均质而统一的。

我们需要做的是将上面两种情况进行综合，曲线与直线连接端来保证过渡的顺畅，而尽可能提到曲线的圆度，即让曲线中间段的部分曲率的变化极为缓和，接近圆的均质统一的曲率特征。

上图 C 就是采用这种策略的一种示意，曲线两头连续过渡，中间部分过渡缓慢，接近均等。

但是上图 C 所示仅为一个粗略的示意，在实际的工作中，要求将会比这更高，比如说对圆度的要求到底是要多高，甚至包括曲率过渡是以怎样的速度或加速度来进行也可能需要在考虑之中，另外也将牵涉到数据的传递，比如从设计到生产，如何来保证形状在传递过程中的保真性。

但我们先否定几个通常对 iOS 圆角图标的猜测。

iOS 圆角图标不是超椭圆

一个有趣的现象是，逆向如果是更多依赖于猜测，会发现结果就是指向自己的假设，而在讨论 iOS 圆角图标是怎样的图标和曲线，或者去拟合产品上的曲线，甲乙丙丁走向不同方向，而且谁都认为自己是正确的，而且一看拟合结果，严丝合缝。

比如 iOS 7 发布不久，有人认为是超椭圆（Superellipse），可能不少人看到超椭圆这个吓人的专业词就认为八九不离十了，而且一看两者相拟合的图，严丝合缝，而且还给出如何在 Photoshop 中使用的指南，但是殊不知平面软件使用的 3 阶贝塞尔曲线，而拟合用到的却是一个 5 次方程式。其实超椭圆从头到尾都是曲线，而没有一条直线段，iOS 7 的圆角图标明显有直线部分，如果连这都能匹配上，可想而知用视觉来判断是否高度拟合是多么不可信。

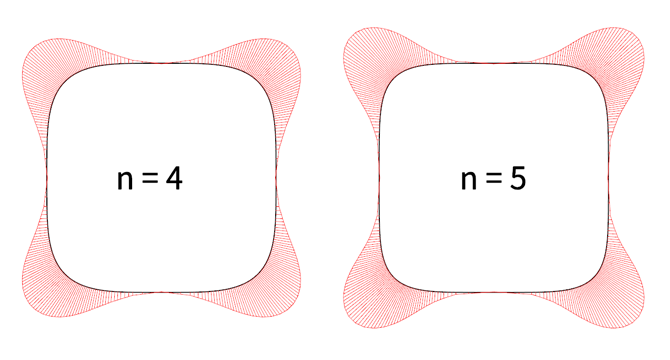
如 Wikipedia 所述，超椭圆是椭圆函数的一般化，即当曲线阶数为 2 的时候为椭圆，当阶数为 4 的时候，如上图左所示为方圆形（Squircle），介于圆和方之间图形（Nokia 的 MeeGo UI 图标被认为是类似 Squircle ），上图右为阶数为 5 的曲线。

从视觉上就能看出超椭圆是曲线，找不到具有圆度的地方，从曲率分布示意图就可以看出，曲率总是在连续过渡，而且阶数越高加速度就越大，即曲率过渡的光滑程度越高。

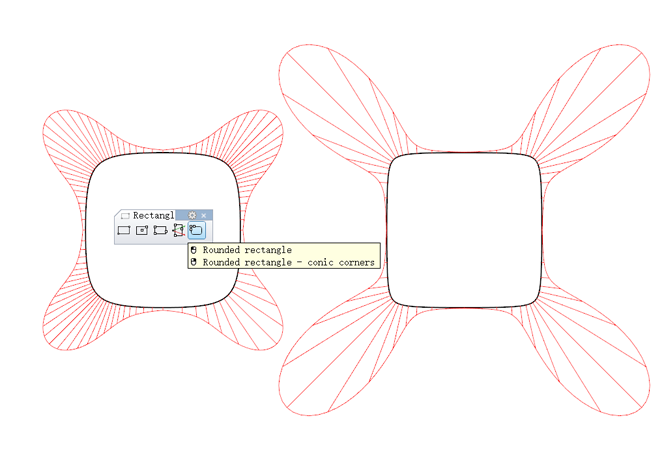
与超椭圆有些类似的是 Rhino 里一个圆角工具（右键点击），圆锥曲线圆角四边形，是用一段圆锥曲线（二次曲线）绘制成 1/4 图形，圆锥曲线圆角四边形的一端极值为圆，而另外一端极值为直角四边形，所以圆锥曲线圆角四边形是不具有圆度的曲线。圆锥曲线因为阶数不高，所以曲线的数学结构较简单，适合绘制一些不圆不方的图形，可以与上面的超椭圆曲线来比较，就会发现圆锥曲线圆角四边形的线条的塑造能力不及高阶的曲线，即一个跨度内曲线的形态塑造能力非常有限，所以除了特殊要求，通常很少用到这一类曲线。另外由于它是二次曲线，所以数据输出的时候需留意。

iOS 圆角图标不是羊角螺线

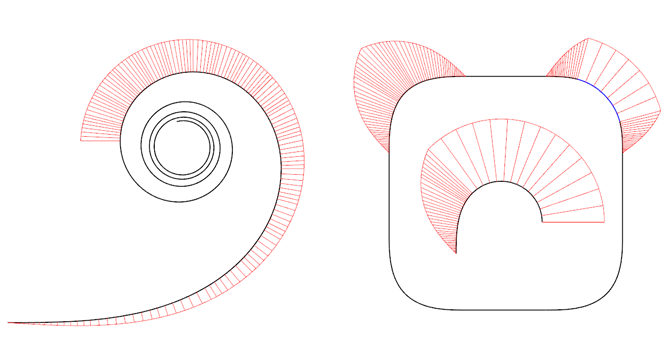
羊角螺线（Euler spiral 或者 Cornu spirals）同上面类似，如果来拟合 iOS 的圆角图标，也可能会达到高度匹配的结果，但实际并不是。

以前羊角螺线常用于公路和铁路工程之上，“以缓和直路线与圆曲路线之间的曲率变化”（Wikipedia 介绍）。而羊角螺线的主要特征是，它的曲率从 0 开始，而且是随着曲线长度（弧长）增大而线性增大，所以当一条羊角螺线的尾部与一个圆形相连时，那么这条曲线肯定是曲率连续的。如上图右所示的两种图形，一条为与圆相连（圆角四边形内部），一条为一段羊角螺线的镜像连接（圆角四边形，左上角），它们都是曲率连续的（G2 连续）。

正因为羊角螺线的这个特性，随着曲线长度的增大曲线呈线性增大，让其具有不少应用之处。在上图右中，虽然我们看到了曲率的变化率曲线（红线）具有尖点和不连续性，但是曲线本身（低一阶次）是光滑连续的。上图右的圆角四边形左上角使用的是一段羊角螺线的镜像连接，它的曲率从 0 线性增大到某个值，然后又降回到 0，按我们上面的基本概念中介绍，这样的曲线是不具有圆度的。

那么羊角螺线既然有这样的特征，我们可以在中间加入一段圆弧，如上图右的圆角四边形的右上角所示，就得到了一个连续的圆角，而且圆度有保证，首尾与直线段也是曲线连续，而且三段曲线形成的圆角的曲率的变化率，虽然不是连续的，但也是非常简单的数学结构，从 0 增大到某一数值，停留，然后再降到 0。而羊角螺线可以用三次曲线来趋近，那么在实际的应用中就有相应的方便之处，比如在平面的矢量绘图软件中使用，来绘制类似 iOS 圆角图标的曲线连续圆角四边形。

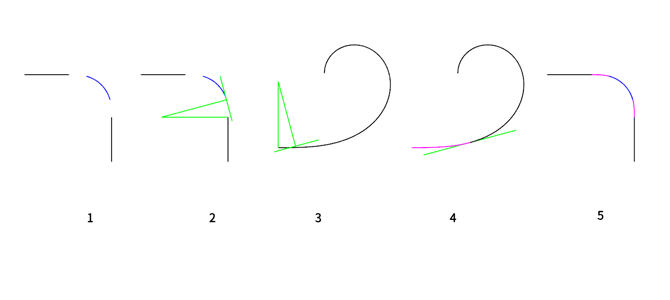
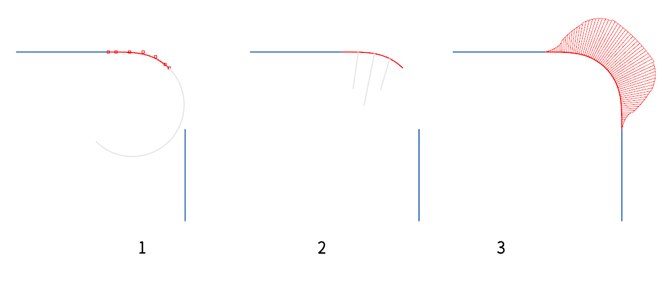
方法是，从 Wikipedia 可以下载到满足使用的羊角螺线矢量图（SVG），然后就是定义圆角曲线中圆弧的大小是多少，然后确定这段圆弧占圆角曲线总长度，也就是画好如上图 1 所示的图形，然后按如图 2 所示画出圆弧一端的切线和法线，并画出直线的垂线，形成一个类三角形，接着将这个类三角形移到羊角螺线之上，定好位置，如图 3 所示，然后移动斜线，找到这条斜线与羊角螺线的相切位置，切断羊角螺线如图 4 所示，得到一段羊角螺线，作放大或缩小动作，装入圆角曲线的圆弧两头，完毕如图 5 所示。

这种绘制方法可以方便地在平面软件内完成，因为目前平面软件没有其他相应的工具来直接或辅助绘制这样的圆角四边形，即保证曲率连续又保证圆度。那么曲线推敲的关键在于确定圆弧段的大小以及占整体曲线长度的比率。

用羊角螺线以这种方式（两端羊角螺线中间圆弧）绘制的圆角四边形的缺点有两个，一个就是形成的整条曲线它的曲率连续但曲率的变化率不连续，第二个就是羊角螺线段的曲率增大是线性的，所以虽然曲率具有加速度但曲率的变化率是恒定的。当对曲线的品质有更高要求时，或者是在三维产品上实现时，不仅对产品的形态还对产品的高光等光学表现有要求时，就可能需要用到更加光滑和连续的曲线了，因为重要的是，这一切的区别都有可能被眼睛看到。

iOS 圆角图标

Apple 的 UI Design Resources 网页上，提供了 iOS 的 UI 素材下载，在素材里面提供了 iOS 圆角图标的矢量图，可以导入各种绘图软件中使用，而且提供的矢量的布点方式和 iOS 7 发布时对圆角图标描述的布点一样，所以这个矢量图的原真性就可以得到确认。

iOS 的圆角图标从宏观上看由 4 条直边和 4 条曲线形成的圆角组成，从圆角曲线的曲率变化示意图中可以看到它符合我们上面说的要求，即首先是曲率连续的曲线，然后能够保证曲线的圆度，让它看起来就像圆弧一样，另外我们也可以看到曲率变化具有加速度，曲率变化的状态大致可以分成五个阶段，第一阶段，也就是接近直线处，以缓慢的速度增加曲率，到达某一值进入第二阶段，也就是快速增长阶段，达到一定程度后，就连续光滑地过渡到第三阶段，以极其平缓的速度变化几乎匀速一般，也就是圆弧阶段，之后的变化过程就是反方向，第四阶段是快速降低，第五阶段是缓慢降低到 0。

在圆角处“缓慢—加速—平缓—加速—缓慢”的变化轨迹是典型的，但具体到应用上亦要看具体情况，并不是做到同 iOS 圆角图标的曲率变化曲线就能符合各种要求的。

iOS 的圆角图标在圆角处的曲线有 11 个分割点分成了 10 段曲线，它们都为 3 阶贝塞尔曲线，如果仔细看这 10 段曲线，会发现它们前后相连并非是严格的曲率连续（G2 连续），看曲率示意图在相邻的两端曲线见，曲率的数值有略微的跳动。并不是形成了尖点，而是有台阶段差，如上图蓝色圆圈处所示，这些台阶段差在每两段前后相连的曲线交点处都能找到，只不过太小在上图无法看出。

虽然再严格的数学意义上来说，这样的曲线连接只能达到切线连续（G1 连续），但是我们谈论是否达到一种标准，还要看公差范围，如果在公差范围内，那么它就是曲率连续。而更为重要的是，我们要从宏观上从视觉上从实际应用中去判断，所以有这样的台阶段差在这对曲线的光滑没有影响。

那么这些线段和段差是如何生成的呢？我们先来分下一下圆角处的曲线。

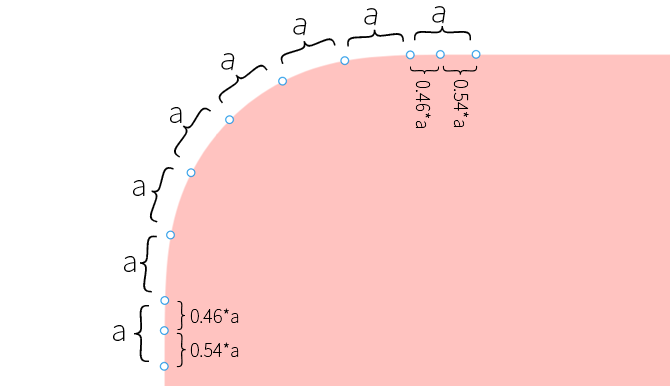
如上图所示，我们对分段的曲线进行测量，测量它的曲线长度（弧长），会发现上图所标的这些线段的长度都是完全一样的，除了靠近直线端的两条曲线段，它是作了再次的分割。

而这个再次的分割，将一段曲线长度为 a 的曲线分成两段曲线，曲线长度分别是 0.46*a 和 0.54*a，这个切割方式看上去很随机，推断有三种可能性：一种为作者留下的签名，可用来追踪（万一被他人侵权使用）或其他作用；第二种可能是留下的干扰因素，来干扰逆向；第三种可能是为了保证数据在传输过程中的安全和保真性。

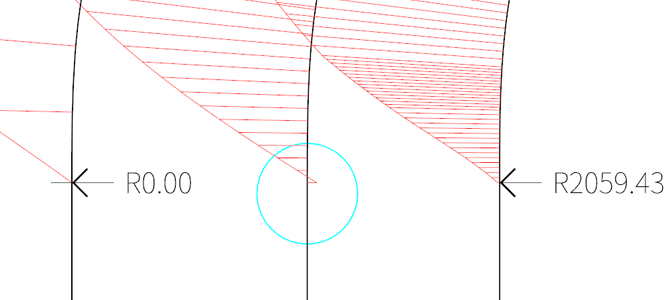
上图是保证数据传递中的安全和保真性的一个例子，第一条曲线为 5 阶曲线与直线曲率连续，所以交点位置的曲率为 0，如果这条曲率连续的曲线不作处理，传递给最高只有 3 阶曲线的软件，那么曲线转化过程中很有可能变成中间这样，如蓝色所示位置曲线弯曲方向发生了变化，为了避免这种转化过程中不必要的错误发生，在一些极值处，比如从 0 开始的变化，将其设置到一个与 0 接近的数值，比如上图所示，可以给其一个非常微弱的曲率。（注：此为个人经验，并未经过理论上的验证）

我们可以不必去追究 0.46*a 和 0.54*a 的由来，因为我们能确定的是 iOS 的这写曲线段的曲线长度（弧长）是均等的，而且都是 3 阶曲线。那么，首先能否定的，这个图形肯定不是设计师一条接一条画出来的，也不是由程序自动生成的，因为这 10 段曲线是太多可能性里面的一种，所以合理的解释就是通过其他曲线，更高阶的曲线，转换为多段的 3 阶曲线，而这个转换过程是以均等曲线长度为依据的，也就达到上述的多段曲线长度为 a 的曲线组成的圆角。

那么为什么不用 3 阶多段的曲线来直接绘制呢？因为 3 阶曲线内部最多只满足 G2 连续，所以无法用它来有效的绘制顺畅的曲线，如果要使用多段的曲线就需要用到高阶曲线，比如 5 阶或 7 阶。

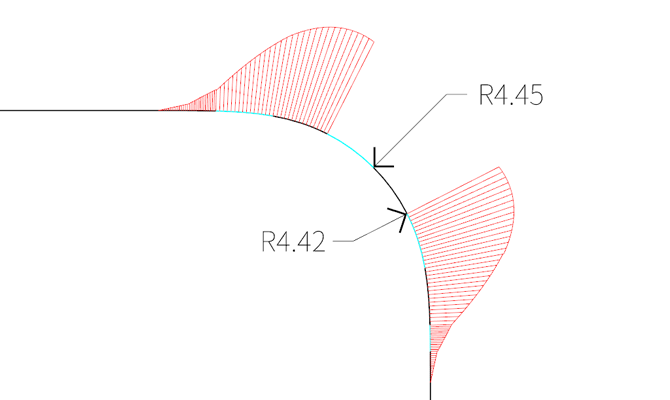
iOS 圆角图标是如何来保证圆度的呢，我们可以看一下圆角部分最中间的两段曲线，按照上面长度的关系，中间两段曲线占总曲线长度的 1/4。我们能看到一段曲线两侧的 R 值有微弱的差别，可以说明这两段设计师就是以圆弧来要求的，但是为什么会不一样，因为是用 3 次曲线来逼近圆弧，如果使用 2 次曲线就可以画出曲率完全均等的圆弧，但是 2 次曲线的引入，将为后续图形的追加以及数据传递带来不可预见的复杂性，在 3D 相关的设计中，绝大多数的场景中，都需用 3 次曲线来绘制圆弧，基本上的软件都提供 3 次曲线绘制圆形的工具。

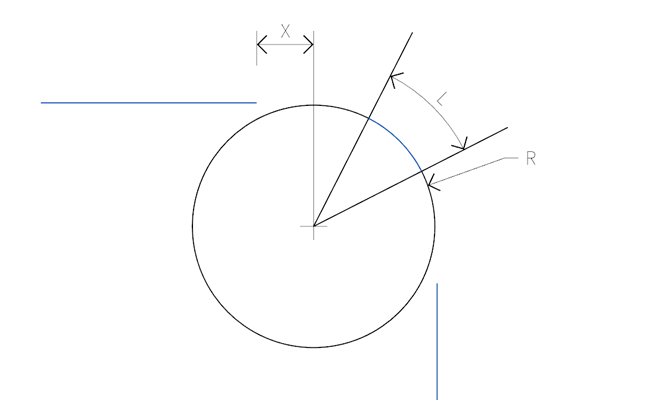
因此，绘制问题就如上图所示，需要事先确定的就是 X、R 和 L 的值，这些数值的确定就是这个圆角的设计工作。X 就是直线一端与圆弧圆心的距离，X 肯定为正值数字，用圆弧来形成的圆角，就是此前提到的 G1 连续圆角，X 值为 0。R 代表的圆角的大小，但因为我们要作的是曲率连续的圆角，使用到的一端圆弧小于 1/4，即上图的 L 值，所以在设计 R 的大小时并不能完全依赖于 G1 连续圆角的感觉。X、R 和 L 值的确定是需要反复推敲，不断画草稿来寻找的过程。

一旦 X、R 和 L 值确定，我们就是怎么来绘制图形的问题了。

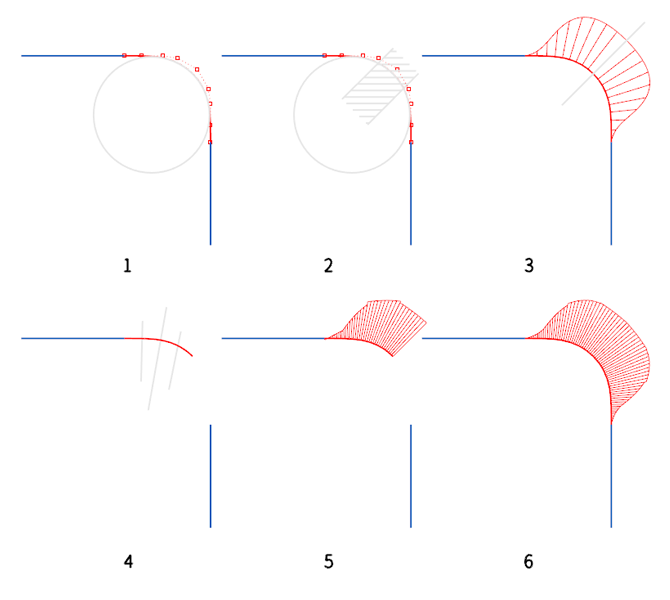
上图是达到 iOS 圆角图标最直接快速的方法。图 1 是在两个直线段之间作一条 7 阶 2 Span 的曲线，即总共控制点有 9 个控制点，7 阶曲线具有很高的塑造性，而且在此处为对称性图形，所以只需要操作 4 个控制点就能完成任务，第 2 和第 3 个控制点受制于曲率连续将与直线共线。图 2 是去拟合圆形，尤其是斜线区域内要做到高度拟合，来回操作控制点。图 3 是当曲线调整到满意后，从中间断开。图 4 是再向下断，将圆角曲线的一半断成均等的 4 等份，得到的 4 段曲线长度相同的 7 阶曲线。图 5 是将这 4 段 7 阶曲线转换为 3 阶曲线（4 个控制点），并且作微调，保证两两相接的曲线切线连续，并且将曲率的段差控制到尽可能小。图 6 就是镜像后的结果。

这个绘制方法的关键点在于拟合圆部分，需要靠操作控制点，亦可借助一些分析工具（比如分析最大最小曲率的差值），让曲线尽可能接近圆形。另外一个要点就是曲线要先分段再降阶，这样可以很好的控制好因降阶带来的形变，如果在第三步直接将完整的 7 阶曲线转为 3 阶 8 段曲线，不仅形状误差会超出允许公差，更糟糕的曲率变化曲线将很难达到光滑。

而这个方法有一个缺点就是圆的拟合部分，需要耗费操作的时间，而且圆角曲线的中点并不在事先给出的确切位置上，改进方法如下。

让一段 5 阶 2 Span 的曲线一端与直线曲率连续，另外一头与中间的圆弧去作曲率连续，其余操作手法类似上一方法，均分曲线段，降至三阶曲线，微调曲率，镜像完成。

以上方法都是指来完成类似 iOS 图标圆角处 10 段曲线的绘制，而实际中有时候并不需要这么复杂，那么可考虑用以下方法。

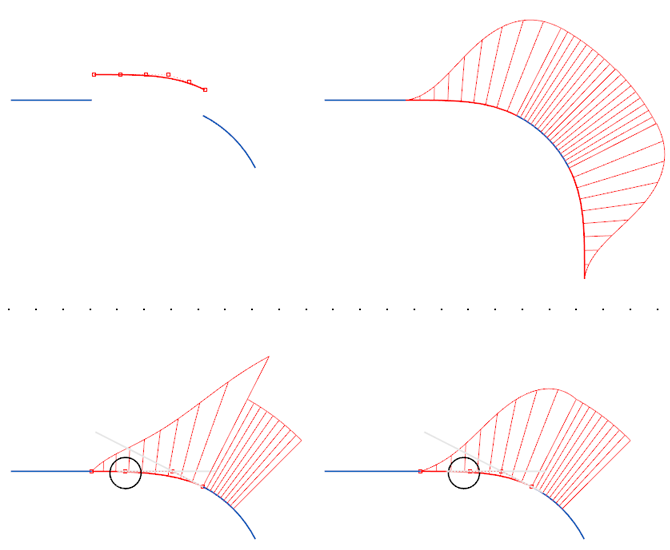
我们已知了三段曲线，那么直接用一条 5 阶的曲线完成直线和圆弧之间的连接，只要调整好曲线的曲率变化即可。

另外也可以用一条 3 阶曲线来完成，当使用 3 阶曲线时，只有一个控制点可供操作，因为另外一个控制点要满足与圆弧连续，又要与直线连续，就必然位于直线的延长线和圆弧端点处切线的交点上，所以可以拖动这个可供操作的控制点，来达到曲率连续，曲率连续的位置点存在并且只有一个，虽然用手拖动操作只能尽可能逼近，但正因为这样的特点，即如果用 3 阶曲线来完成直线和圆弧之间的曲率连续，这条 3 阶曲线是确定的，所以可以用算法来完成求解，前提是前面说到的 X、R 和 L 值确定。在但 X、R 和 L 值确定的情况下，用此方法来形成三段曲线的连接，有时效果未必很好，比如上图右下所示的 3 阶曲线段，曲率的最大值出现在内部而不是尾部，这将影响到曲线的质量，如果此情况下 X 值可以变动，即这条 3 阶曲线与直线连接位置可以微调，可能会带来较好的效果。

尽管用 3 阶曲线来完成圆角曲线的绘制相对简单，只需要动一个控制点，但在平面软件中来绘制，因为缺少曲率分析和呈现的模块，所以还是难以实现操作。

前 Apple 出色的交互设计师 Bas Ording（就像 iOS 时代的 Bill Atkinson 一样）在 2013 年申请了一项专利（2016 年获准）US9396565，专利名称是“用户图形界面元素中边界的渲染”，专利内容就是用 3 阶曲线来绘制圆角四边形，而基础正是基于这条 3 阶曲线的 4 个控制点具有约束性。

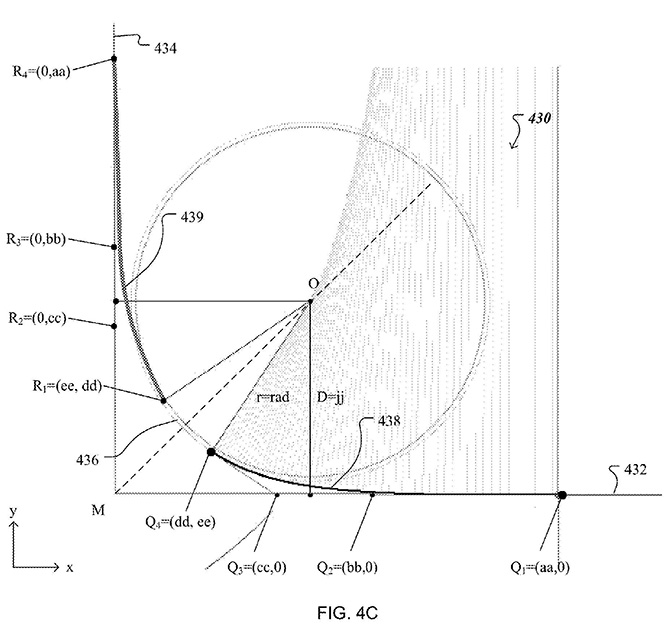
Bas Ording 采用算法来完成，基于 3 阶曲线与两段的直线和圆弧形成曲率连续后，这条 3 阶曲线的控制点位置的特征。他的圆角生成需要先输入圆弧段的半径，以及圆弧两边两条非圆弧曲线占圆角曲线整体弧长的比率，以这两项参数输入就可以生成圆角曲线，如果在输入四边形的长和宽，就可以生成圆角四边形。他的算法我并没全看明白，而他给出的结果是上图中的 Q2Q1 间的距离是 Q3Q2 的两倍，就可以看出这个算法并不能一般化（开始就设定了一个固定比率），只是涵盖了某一个子集的曲线，可能他在计算过程中加入了其它限定因素。

以上是关于 iOS 圆角图标及其实现的方法，只针对于平面的图形效果，如果来绘制一条手机的轮廓线，肯定不会使用 iOS 圆角图标那样分成 10 段 3 阶曲线，那将是另外一个更复杂的生成环境，数据的传递和实现就有更长的路径。

圆角是一个小细节，就跟设计本身一样，如果不在意，就没必要大费周章，但如果在意这些细节，在意曲线的质量，那追求是无止境的。